Teaching

Teaching Experience and Course Information

Multidisciplinary Design Optimization (MDO)

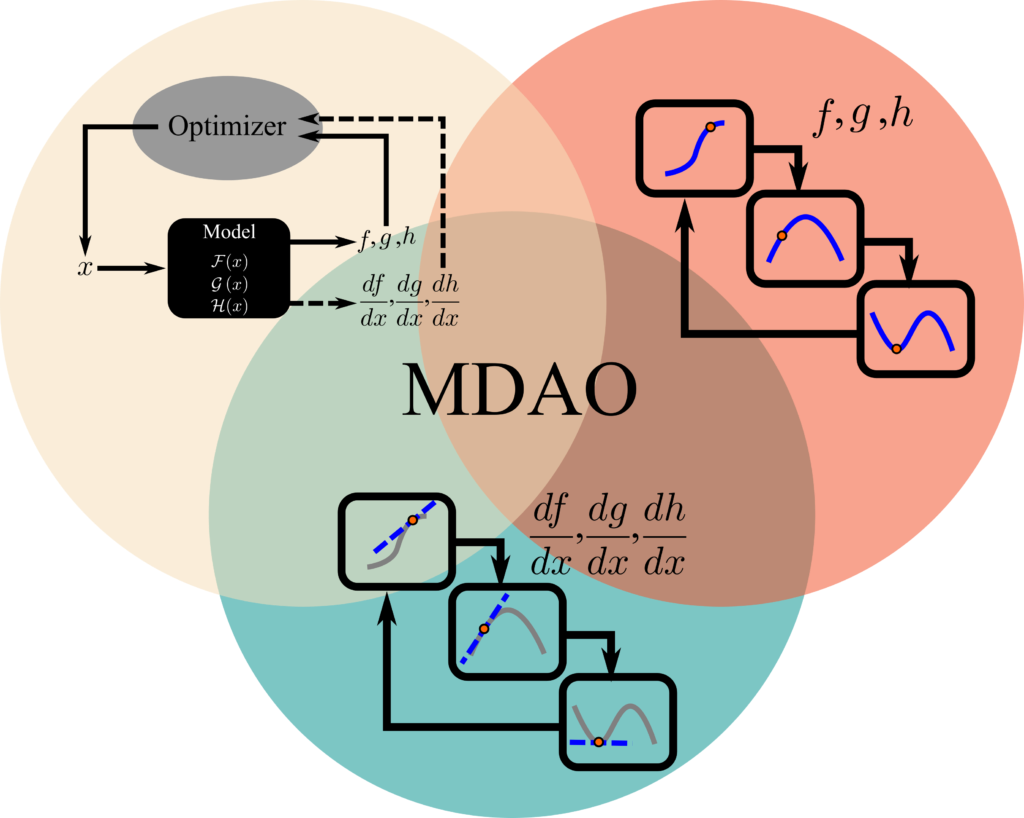Image: openmdao

Course: Multidisciplinary Design Optimization
Institution: Cornell University
Role: Teaching Assistant
When Offered: Fall Semester
Prerequisites: Undergraduate linear algebra and knowledge of MATLAB, Python, or R

Course Overview: This course presents a rigorous, quantitative multidisciplinary design methodology that incorporates the creative side of the design process. Through a topic of your choice, students learn how to use multidisciplinary design optimization (MDO) to create advanced and complex engineering systems that must be competitive in performance and life-cycle value.

Key Focus Areas: -Multidisciplinary character of engineering systems -Design of complex systems
-Tools for optimization

Course Structure: Students work in small teams on a term project to apply MDO principles to design and optimize an engineering system of their choice.

Learning Outcomes

Students who successfully complete this course will be able to:

  1. System Decomposition: Subdivide a complex system into smaller disciplinary models, manage their interfaces and reintegrate them into an overall system model.

  2. Algorithm Selection: Identify the most suitable optimization algorithm between gradient-based numerical optimization algorithms (i.e., sequential quadratic programming (SQP)) and various modern heuristic optimization techniques (i.e., simulated annealing (SA) or genetic algorithms (GA)) for their design problem and use it to find the optimal design for a single objective of their choice.

  3. Critical Analysis: Critically evaluate and interpret analysis and optimization results, including sensitivity analysis and exploration of performance, cost and risk tradeoffs.

  4. Multi-Objective Optimization: Utilize basic concepts of multi-objective optimization, including the conditions for optimality and Pareto front computation techniques, to optimize their design with respect to two objectives of their choice.

  5. Team Project: Work as a team to formulate a realistic engineering design problem, optimize the design for a single objective and multiple competing objectives, and present the results in a final oral presentation and written report.

Course Philosophy

This course is fundamentally different from most traditional university optimization courses which focus mainly on the mathematics and algorithms for search. The focus is equally strong on all three aspects of the problem:

  • Multidisciplinary Integration: Understanding how different disciplines (structures, aerodynamics, controls, optics, costing, manufacturing, environmental science, marketing, etc.) must be tightly coupled during conceptual and preliminary design of complex new systems and products.

  • System Design: Developing the ability to design complex engineering systems that are competitive in performance and life-cycle value.

  • Optimization Tools: Mastering both gradient-based and heuristic optimization techniques for real-world engineering applications.

Technical Skills Covered

  • Programming: MATLAB, Python, or R for implementation
  • Optimization Algorithms:
    • Gradient-based methods (Sequential Quadratic Programming)
    • Heuristic methods (Simulated Annealing, Genetic Algorithms)
  • Multi-objective Optimization: Pareto front computation and analysis
  • Sensitivity Analysis: Understanding design parameter impacts
  • System Integration: Managing multidisciplinary model couplings

This course provides students with practical experience in applying MDO principles to real engineering problems, preparing them for careers in advanced engineering design and optimization.